尾递归实现foldRight

发表于   |     |   阅读次数

什么是尾递归

尾递归是指递归调用作为函数执行的最后一条语句，这样的情况下递归调用发生时，当前的栈帧就不需要了。如果语言有对尾递归做这样的优化，那么不论尾递归调用多少层，都不会有栈溢出的风险。特别注意的是，类似于下面这样的代码不是尾递归的，因为它执行的最后一条语句是 h + sum_result 而不是 sum(t) ，换句话说，这里调用 sum 时，栈帧还不能抛弃，因为栈帧中还需要保存 h 。
更详细的介绍请看： https://zh.wikipedia.org/wiki/%E5%B0%BE%E8%B0%83%E7%94%A8

1
2
3
4
def sum(list: List[Int]): Int = list match {
  case Nil => 0;
  case h::t => h + sum(t)
}

非尾递归的实现

1
2
3
4
def foldRight2[E, B](l: List[E], b: B)(op: (E, B) => B): B = l match {
  case Nil => b
  case h::t => op(h, foldRight(t, b)(op))
}

以上代码以一种最容易想到的方法实现了 foldRight， 但是很遗憾，它不是尾递归。::方法是常量时间完成，不涉及递归，后面不再解释。递归调用 foldRight 返回后还需要使用 h 和递归结果作为参数调用 op，栈帧中还需要保存 h 和 op，所以以上实现不是尾递归的。

尾递归的实现

虽然直接实现 foldRight 的尾递归版本有困难，但是 foldLeft 却很容易用尾递归实现。那我们实现一个尾递归的foldLeft，然后翻转 list 调用 foldLeft ，以此来实现 foldRight ，这样可行吗？下面试试看。

尾递归的 foldLeft

1
2
3
4
def foldLeft[E, B](l: List[E], b: B)(op: (B, E) => B): B = l match {
  case Nil => b
  case h::t => foldLeft(t, op(b, h))(op)
}

以上实现，最后执行的代码就是对foldLeft的递归调用，栈帧中需要保存任何信息，显然是尾递归的。

使用 foldLeft 实现 foldRight

1
2
3
4
def foldRight[E, B](l: List[E], b: B)(op: (E, B) => B): B = l match {
case Nil => b
case h::t => foldLeft(reverse(l), b)((b, e) => op(e, b))
}

这样就完了吗？当然没有，上面的实现使用了reverse函数，得尾递归实现reverse才行

尾递归实现reverse

这里就不卖关子了，直接使用 foldLeft 来实现 reverse 就可以了。

1
2
3
4
def reverse[E](l: List[E]): List[E] = l match {
  case Nil => Nil
  case h::t => l.foldLeft(Nil:List[E])((b, e) => e::b)
}

结果检验

上面有了 foldRight2 和 foldRight 两个实现。我们用一个长 list 来分别调用两个函数看看是否栈溢出。

1
2
3
4
5
6
7
object App {
  def main(args: Array[String]): Unit = {
    def bigList = 1.to(10000).toList
    println(foldRight2(bigList, 0)((e, b) => e + b))
    //println(foldRight(bigList, 0)((e, b) => e + b))
  }
}

上面使用了一个长度为10000的 list，计算所有元素的和。
使用 foldRight2 时发生了栈溢出，根据jvm启动参数的不同，发生栈溢出的临界值是不一样的。

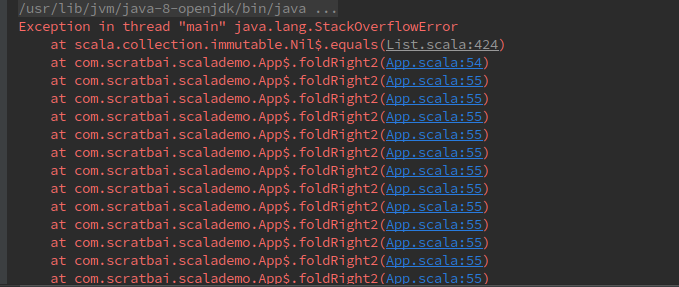
Alt text

使用 foldRight 时正确输出了结果

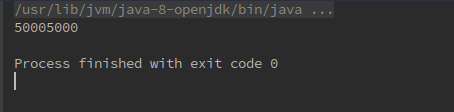
Alt text

说明这里的尾递归实现是正确的，并且Scala的做出了正确的优化。